2025高考志愿AI填报系统(开放)
安徽
请选择科目
1.
把一个正四面体的每个表面都分成9个相同的等边三角形,用任意颜色给这些小三角形上色,要求有公共边的小三角形颜色不同,问:最多有多少个小三角形颜色相同?( )
A.15
B.12
C.16
D.18
2.
三角形的内角和为180°,问六边形的内角和是多少度?( )
A.720
B.600
C.480
D.260
3.
A.4
B.6
C.8
D.10
4.
某工程队给一个长方形广场铺地砖,已知每平方米铺设成本为25元,若广场的宽不变,长增加5米,总成本则上升1.25万元;若广场的长不变,宽增加3米 ,总成本则上升1.5万元。则广场原来铺设的总成本为( )万元。
A.50
B.60
C.70
D.80
5.
一个等腰三角形,一边长是30厘米,另一边长是65厘米,则这个三角形的周长是( )
A.125厘米
B.160厘米
C.125厘米或160厘米
D.无法确定
查看答案与解析
[page]
1.答案: A
解析:
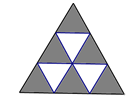
如上图所示,假定四面体中的其中一个面的9个等边三角形中有6个三角形的颜色相同,则其他每个面最多有3个等边三角形颜色可以相同,则一共有6+3×3=15个。因此,答案选择A选项。
2.答案: A
解析:

3.答案: A
解析:
从最少的情况考虑,如下图所示即可实现。 右图为俯视情况,其中阴影表示放置有立方体的位。
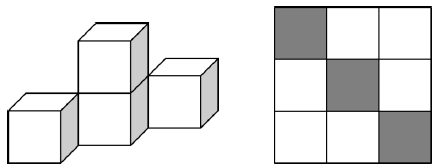
故正确答案为A。
4.答案: A
解析:
设长为a米,宽为b米,由题意可知25*(a+5)*b=25ab+12500 25a*(b+3)=25ab+15000 解得a=200,b=100,则总成本为25*200*100=500000元=50万元。故答案选A。
5.答案: B
解析:
已知该三角形是等腰三角形,由三角形任意两边的和大于第三边可知,另一条腰为65cm,因为30+30<65,则其周长为30+65+65=160厘米。故正确答案为B。
再来15题
输入分数,查看能上的大学
安徽
请选择科目

