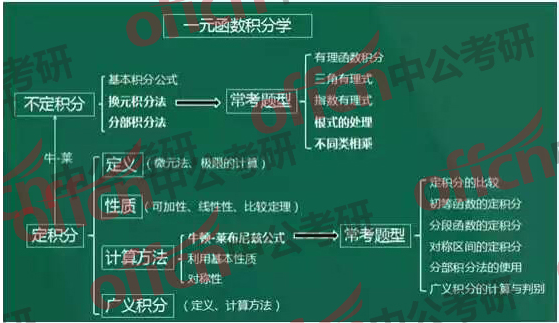
历年来考研数学都是同学们比较头疼的一门科目,同学们总会说数学好难呀,怎么也学不会。但是想一想,每年又都会有满分高分大神,因此数学虽然难但也一定是有方法技巧可寻的。
中公考研数学名师李擂老师为同学们总结了考研数学各科目的思维导图,旨在帮助同学们梳理考研数学中的重要考点,下面根据李擂老师的思维导图,中公小编为同学们整理了高等数学一元函数积分学的核心考点解析。希望可以帮助到大家。
【一 基本积分公式】
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
考研数学复习,公式是基础也是关键,熟练灵活的掌握公式才能得心应手的做出各类型题目,高等数学中公式众多,大家要加深理解记忆。下面带着大家一起来巩固熟悉高等数学中基本积分公式。
2017高数核心考点之基本积分公式 |
【二 换元积分法】
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
换元积分法是求积分的一种方法。它是由链式法则和微积分基本定理推导而来的。主要有两种方法:第一类换元法与第二类换元法。
2017高数核心考点之换元积分法 |
【三 分部积分法】
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
分部积分法是微积分学中的一类重要的、基本的计算积分的方法。它的主要原理是利用两个相乘函数的微分公式,将所要求的积分转化为另外较为简单的函数的积分。
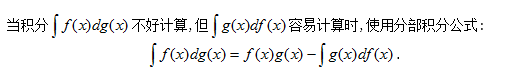
2017高数核心考点之分部积分法 |
【四 常考题型】
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
我们已经在前面的部分中了解了定积分的基本积分公式与两种积分方法,而仅仅掌握知识点还不够,我们需要对这几个内容灵活运用,下面就让我来看一下关于定积分的五大常考题型吧!
有理函数积分 |
有理函数就是通过多项式的加减乘除得到的函数。 一个有理函数h可以写成如下形式:h=f/g,这里 f 和 g 都是多项式函数。有理函数是特殊的亚纯函数, 它的零点和极点个数有限。 有理函数全体构成所谓的有理函数域。 在实数范围内,无限不循环的小数叫做无理数,一般通过开平方得到。在二次函数里面,如 y=a*x^2+b*x+c,如果△≥0,那么 y=0 有实数解;如果△<0,那么 y=0 没有实数解,但有虚数解。 |
不定积分常考题型有理函数积分 |
三角有理式 |
三角函数有理式是指由三角函数和常数经过有限次四则运算所构成的函数,记作:R (sin x,cos x) |
不定积分常考题型三角有理式 |
指数有理式 |
当被积函数中含有指数函数时,用代换可转化积分形式,但常常需要配合其他变换。 |
不定积分常考题型指数有理式 |
根式的处理 |
被积函数为简单根式的有理式,可通过根式代换化为有理函数的积分。 |
不定积分常考题型根式的处理 |
不同类相乘 |
不同类积分相乘是几种题型中相对复杂的一种,需要同学们选择好u与dv,若选取不当,将无法得出结果。 |
不定积分常考题型根式的处理 |
【一 定积分的定义】
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
定积分是积分的一种,是函数f(x)在区间[a,b]上的积分和的极限。这里应注意定积分与不定积分之间的关系:若定积分存在,则它是一个具体的数值(曲边梯形的面积),而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式),其它一点关系都没有!一个函数,可以存在不定积分,而不存在定积分,也可以存在定积分,而不存在不定积分。一个连续函数,一定存在定积分和不定积分;若只有有限个间断点,则定积分存在;若有跳跃间断点,则原函数一定不存在,即不定积分一定不存在。
2017高数核心考点之定积分的定义 |
|
极限的计算 |
微元法 |
【二 定积分的性质】
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
定积分的性质主要包括三方面:可加性、线性性、比较定理。下面就让我们具体看一下吧。
2017高数核心考点之定积分的性质 |
【三 定积分的计算方法】
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
定积分主要有三种计算方法:牛顿-莱布尼兹公式、利用基本性质以及利用对称性,其中牛顿-莱布尼兹公式是最常用也是相对简便的方法。
牛顿-莱布尼兹公式通常也叫做微积分基本公式。它表示一个函数定积分等于这个函数的原函数在积分上、下限处函数值之差。它揭示了定积分和不定积分的内在联系,提供了计算定积分有效而简便的方法,从而使定积分得到了广泛的应用。
2017高数核心考点之定积分的计算方法 |
【四 广义积分】
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
在一些实际问题中,常遇到积分区间为无穷区间,或者被积函数为无界函数的积分,它们已经不属于前面所说的定积分了。因此,我们队定积分作了推广,从而形成广义积分的概念。
广义积分的定义 |
广义积分的计算方法 |
【五 常考题型】
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
我们已经在前面的部分中了解了定积分的定义、性质以及计算的基本方法相关知识点,而仅仅掌握知识点还不够,我们需要对这几个内容灵活运用,下面就让我们来看一下关于偏导数的六大常考题型吧!
分部积分法的使用 |
广义积分的计算与判别 |
初等函数的定积分 |
定积分的比较 |
对称区间的定积分 |
分段函数的定积分 |

